Graph Theory

Graph Theory is an essential part to computer science and competitive programming. I wanted to make sure we introduce the basic of graphs before delving into more sophisticated applications.
For a comprehensive look at graph theory, follow gladius’s series of blogs on graph theory and chapter 11 onwards of this goat book. We will use DarthKnights’s implementations as well as this library for code.
From this point on, I assume you know these basic facts about graph:

• Definition of a graph, vertex, and edge. What it means for a graph to be undirected, directed, or weighted. What is a multi-graph, bipartite graph, and regular graph.
• Definition of a path, walk, cycle, component, degree, adjacency, etc.
• Alternative definitions of a tree, subtree.

Representation of a graph

There are generally two ways to represent a graph: adjacency matrix and adjacency list. Adjacency matrix refers to a matrix where adj [ i ] [ j ] is 1 if there exist an edge between i and j (in a weighted graph, adj [ i ] [ j ] will be the weight of the edge between i and j). Adjacency list refers to an array of lists where adj[ i ] is a list of all elements adjacent to i. In some cases (mostly in weighted graph or a flow network), we also make adj [ i ] refer to a list of edges incident to i.
Adjacency list can replace its matrix counterpart in almost any situation, so all the implementation and analysis featured here will be focused mainly on this representation.
The following is an implementation of Adjacency list:

int N; // the size of the graph
vector<int> adj[maxN]; // the adjacency list

void addEdge(int i, int j) {
 adj[i].push_back(j);
  adj[j].push_back(i);
}

In a weighted graph, it is best to make the adjacency list lists the edges incident to a vertex v. This reduces the need to implement an edge structure. This approach is also used in flow-network problems (don’t worry if you don’t know what this is yet), since you can’t easily alter objects stored in a vector.

int N; // the size of the graph
vector<int> adj[maxN]; // the adjacency list
int a[maxM], b[maxM], c[maxM]; // edge e from a[e]<->b[e] with weight c[e].

// use xor to retrieve the adjacent vertex
int other(int e, int v) { return a[e]^b[e]^v; }

Graph traversal

There are two types of traversals on an unweighted graph: dfs (depth first search) and bfs (breadth first search). As the name implies, Depth first search tries to traverse the tree by depth, and go as far as possible before backtracking and exploring other paths. Breath First Search explore vertices in a graph by order of distance from a root vertex (where we start the search).
Visually:

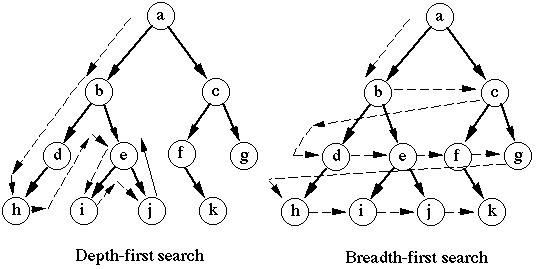
Dfs works slightly faster and is more natural to code since you can use recursion to reduce the need for an explicit stack. Bfs, however, requires a queue, and so is a little more lengthy in implementation. Additionally, it has some cool properties like giving you the shortest distance from the root to any node in an undirected graph.
This is an implementation of dfs:

void dfs(int v) {
  vis[v] = 1; // vis is an array denoting whether a vertex has been visited
  for (int w : adj[v]) 
    if (!vis[w])
      dfs(w);
}

And this is one for bfs:

void bfs(int s) {
 queue<int> pq;
  pq.push(s);
  d[s] = 0; // d[v] denotes distance from v to s. Initially, d[v] = oo = infinity
  
 while (!pq.empty()) {
  int v = pq.pop_front();
    for (int w : adj[v])
      if (d[w] == oo) 
        d[v] = d[w]+1, pq.push(v);
 }
}

For more on the subject, read chapter 12 of the goat book.

Enough with the theory! I want practice

Here are a series of problems to get you started with dfs. All of these are non-standard problems (if you want standard the best way is look into textbooks).

Cut them all

Statement: given a tree of $N$ vertices ($ N \le 10^5$), find the maximum number of edges you can remove such that all remaining components have even size.
[Source]

Let’s approach this problem by stating the obvious: this is impossible to do if $N$ is odd. The even-size part of this problem is particularly interesting. By property of an even number, if you have two even number $a$ and $b$, then $a-b$ is guaranteed to be even.
We can formulate this in terms of the tree. Let’s arbitrarily root the tree. If we have a tree of size $N$ where $N$ is even, and a subtree in that tree of size $M$ where $M$ is even, we can safely detach that subtree and the tree would still be even. This means if a subtree has even size, we can just remove the edge from it and its parent, since not removing the subtree does nothing to the parity of the size of the parent.
We can find subtree size by dfs, and if it is even we simply detach the subtree.

// we are only interested in the parity of the subtree size, so this function returns 1 or 0
int dfs(int v, int p) {
  int sz = 1;
  for (int w : adj[v])
    if (w != p) // if a vertex is not v's parent
      sz ^= dfs(w,v); 
  if (!(sz&1) && p!=-1) ans++; // add 1 edge to the answer if the size of the subtree is even 
                // and if the node isn't the root
  return sz;
}

Valid BFS

Statement: given a tree of $N$ vertices ($N \le 2 \cdot 10^5$) and a sequence of $N$ nodes. Find if the sequence is a valid bfs. The root node (1) is the source of the bfs.
[Source]

To do this problem, we need to understand the properties of the bfs procedure. For once, if you list the nodes visited by bfs in order, the nodes with a specific distance K from the root forms a continuous sequence, and the nodes further from the root are towards the end of the sequence.
This can serve as our initial check for whether or not the sequence is a valid bfs sequence. However, such a check is not sufficient. Let’s examine the graph:
The sequence [A, C, B, D, F, E] doesn’t fail our distance criteria. However, it is impossible for any bfs scheme to produce this sequence. Since the bfs visits B before it does D, it will explore B’s children before D’s.
Right now, you are probably thinking of a really complicated greedy scheme for determining a valid bfs sequence. Such a scheme might exist, but often times in competitive we favor more elegant ways to solve problems given that time is precious. Why don’t we simply use bfs to solve this problem? Specifically, we sort the adjacency list of every node by the nodes’ apperance in the sequence given. Then we run bfs and if the sequence we get from bfs agrees with the input, then the input is valid.
This turns out to be the most effortless way to approach this problem. The intuition behind why this works is obvious, but proving that it does might be hard.

Garland

Statement: Given $N$ lamps and which lamp they hang on ($N \le 10^6$). Each lamp has a temperature $|t_i| \le 100$. Produce one way to cut the connection between 2 lamps (cut the wire that connects that lamp with whichever it is hanging on), such that the entire structure is cut into 3 parts with the same total temperature.
[Source]

First of all, we need to identify what type of graph models the structure perfectly. Upon further inspection we notice that the definition of lamps is similar to that of a tree. We want to cut 2 edges from the tree so that there are 3 connected components with the same total value.
Your first thought might be to find the total temperature $T$ and two nodes such that the subtree size of node $v$ and $w$ are both $\frac{T}{3}$. However, this general approach has a counter case where $v$ is the ancestor of $w$.
Let’s try another approach based on dfs. If we know that $v$ has a subtree sum of $\frac{T}{3}$ and that no child of $v$ has such subtree size, we can simply remove the edge between $v$ and its parent and count $v$ as one of the two nodes required. After this, we simply return 0 to the parent. This deals with the edge case mentioned earlier.

int dfs(int v, int p) {
 int sum = t[i];
  for (int w : adj[v])
    if (w!=p)
      sum += dfs(w,v);
  if (sum[v] == T/3 && p != -1) {
    // mark v as an answer
    return 0;
  }
  return sum;
}

Components of Graph

As you know, a component in a graph is a collection of vertices such that there is a path between any pair of them. We can use dfs or bfs to find which component each node belongs to. This approach, using dfs, is generally refered to as floodfill because it is similar to pouring water into a vertex and waiting to see which vertices the water flows to.

void dfs(int v, int c) {
  comp[v]=c;
  for (int w : adj[v]) 
    if (comp[w]==-1)
      dfs(w,c);
}

for (int v = 0, c = 0; v < N; v++)
  if (comp[v]==-1)
    dfs(v,c++);

Sometimes decomposing graphs into components allows you to better solve the problem.

Some practice problems

Here are some problems that relates to connected components. Not all of them are straightforward components, but thinking in terms of components reveals interesting facts about each of these problems.

Lunar New Year and a Wanderer

Statement: Given a graph of $N$ vertices and $M$ edges ($N,M \le 10^5$). Bob is having a walk on the graph and he starts at 1 and records a vertex if this is the first time he arrives at that vertex. Bob wants to visit every vertex (recall that since this is a walk, he can visit vertices twice). Of all the ways he can perform the walk, find the lexicographically least sequence of vertices that he will record.
[Source]

Notice that if we think of the vertices that Bob has visited as a component, then the next node that Bob will record must be adjacent to that component (there is an edge between a node in the component to it). We start with a component of only node 1. Now we can greedily just choose the lowest node connected to that component to visit next. If we continue with this scheme, we will produce the answer.

vector<int> solve() {
 vector<int> answer;
  priority_queue<int, vector<int>, greater<int> > pq;
  pq.push(1); vis[1]=1;
  while (!pq.empty()) {
    int v = pq.pop();
    answer.push(v);
    for (int w : adj[v]) 
      if (!vis[w])
        pq.push(w), vis[w] = 1;
  }
  return answer;
}

0-1-Tree

Statement: Given a tree of $N$ vertices ($N \le 2 \cdot 10^5$) where each edge has either number 0 or 1. A pair of vertices $x, y | x \neq y$ is valid if the path $P_{x,y}$ never go through a 0-edge after going through a 1-edge. Find the number of valid pairs.
[Source]

Let’s think about this graph as components. Two nodes are k-connected if node i and node j are connected through a path of edges with weight k. Realize that since the graph is a tree, $x$ and $y$ are either 0-connected, 1-connected, or unrelated, but not both.
Say that a 0-connected component X and a 1-connected component Y are adjacent if they share a node. We realize that now any pair $x, y | x \in X, y \in Y$ is a valid pair. So if we find all the k-connected components, let $z[x]$ be the 1-connected component that $x$ is in and $o[z]$ the 0-connected component, each node $v$ contributes $sz_z [z[v]] \cdot sz_o [o[v]] - 1$ to the total answer (the negative one is to prevent $v$ from pairing with itself).
Finding these values can be done by either floodfill or union find if you are lazy.

Edgy Tree

Statement: Given a tree of $N$ nodes ($N \le 10^5$) and an integer $K$ ($K \le 100$). Each edge in the tree is either red or black. A superwalk is a sequence $[a_1, a_2, a_3, …, a_k]$ that denotes a walk. A person following a superwalk would start at $a_1$ then walk the unique path (since it is a tree) to $a_2$, then to $a_3$, etc. In the process of following the superwalk, a person walks a black edge, then the superwalk is called a good superwalk. Find the number of good superwalks of the graph modulo $10^9+7$.
[Source]

Finding the number of superwalks is relatively easy, since it is equivalent to finding the number of sequences $[a_1, a_2, a_3, …, a_k]$, which is $ n^k$. Now finding the number of good superwalks explicitly requires fancy dp techniques and preprocessing of the graph, all of which are more complicated than neccessary. We will proceed to find the number of bad superwalks and subtract it from the total.
What kind of superwalk is bad? A bad superwalks walks only through red edges. Therefore, we realize that a superwalk is bad if all of its nodes are in a red-component consisting of all nodes connected by paths of red edges. With this, we have our answer: $f(G, k) = n^k - \sum_{c \in comp} {sz[c]^k}$.

Related Problems

These are the problems that relates to the topic.

Easy:

• Vasya and Isolated Vertices
  
• Hongcow builds a nation
  
• Party
  

Medium:

• Substring
  
• Two Paths
  
• Connected Components
  

Hard:

• Connected Components?
  
• Labyrinth
  

Written with StackEdit.